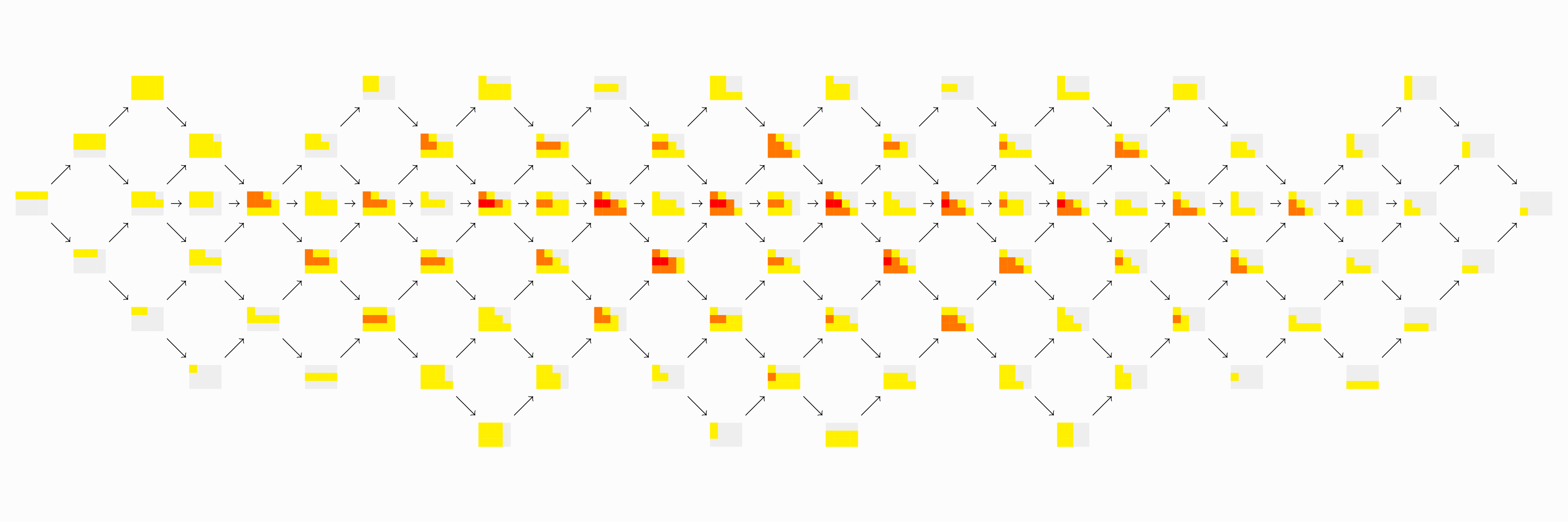
In representation theory, we study algebraic structures by representing their elements as linear transformations of vector spaces. A practical instance of this philosophy can be witnessed in topological data analysis: Here data, say in the form of a point cloud, is turned into a sequence of vector spaces. If we want to preserve any additional information, then the relevant problems in representation theory quickly become insolvably hard.

In our project, on the one hand we studied combinatorial aspects of representation theory – that is aspects that can be approached more concretely – from a purely algebraic point of view. On the other hand we worked with experts on topological data analysis to understand what information they would like to find in the algebraic structures.

In additional to multiple concreate mathematical research results on both sides of the project, one definitive positive effect of our program at CAS for future research is the increasing cooperation between pure representation theory and topological data analysis.